Alteração das
equações da modelagem
Na semana passada, no dia
11/06/19 nos reunimos com o monitor Pedro para dar prosseguimento ao nosso
trabalho. Após um tempo discutindo qual seria a melhor maneira para definirmos
nossas equações, chegamos a um consenso e concluímos que deveríamos equacionar a
modelagem utilizando os seguintes termos:
P – População;
J – Número de usuários de
transporte público a cada 1000 pessoas;
K – PIB (produto interno bruto);
V- Número de veículos
Sendo que:
Onde δ é taxa de natalidade, β
taxa de mortalidade e γ taxa de imigração.
Para encontrar o valor de P, ou
seja, a população utilizaremos o modelo Wonderland. Apesar de ser mais complexo
é facilmente adaptado além de conseguir prever as possíveis interações entre a
economia, a mudança demográfica e o meio ambiente, por exemplo.
No modelo linear, a suposição
básica é que a variação do número total de indivíduos é constante. Em outras palavras,
admite-se que o acréscimo (ou decréscimo) da quantidade de indivíduos por
unidade de tempo não varia com o tempo. Além disso, supõe-se que não há
restrições nem tampouco limitações para o crescimento (ou decrescimento), e,
dessa forma, a população cresce (ou decresce) ilimitadamente.
Entretanto, na modelagem de
crescimento populacional, nem sempre é razoável supor que a quantidade de
indivíduos acrescida na população é constante. Esta suposição pode ser válida
para um determinado período de tempo ou para alguma população em particular.
Admitindo que o número de indivíduos que é acrescido depende, por exemplo, do
tamanho da própria população, o modelo linear não é mais adequado.
Esse modelo envolve muitas variáveis e por
isso optamos por desenvolver nossas próprias equações (mostradas acima) de
acordo com a relação entre os parâmetros.
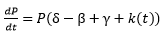


Comentários
Postar um comentário